Distribusi Frekuensi

A.  Pengertian Distribusi Frekuensi

Data yang diperoleh dari suatu penelitian yang masih berupa random dapat disusun menjadi data yang berurutan satu per satu atau berkelompok, yaitu data yang telah disusun ke dalam kelas-kelas tertentu. Tabel untuk distribusi frekuensi disebut dengan Tabel Distribusi Frekuensi atau Tabel Frekuensi saja. Jadi, distribusi frekuensi adalah susunan data menurut kelas-kelas interval tertentu atau menurut kategori tertentu dalam sebuah daftar. Distribusi Frekuensi adalah pengelompokkan data ke dalam beberapa kategori yang menunjukkan banyaknya data dalam setiap kategori, dan setiap data tidak dapat dimasukkan ke dalam dua atau lebih kategori. Distribusi frekuensi adalah susunan data dalam bentuk tunggal atau kelompok menurut kelas-kelas tertentu dalam sebuah daftar.

Menurut Hasan, distribusi frekuensi adalah susunan data menurut kelas-kelas tertentu (2005: 41). Sedangkan menurut Suharyadi dan Purwanto, distribusi frekuensi adalah pengelompokan data ke dalam beberapa kategori yang menunjukkan banyaknya data dalam setiap kategori, dan setiap data tidak dapat dimasukkan ke dalam dua atau lebih kategori (2003: 25).

Tujuan distribusi frekuensi ini, yaitu :

1. Memudahkan dalam penyajian data, mudah dipahami, dan dibaca sebagai bahan informasi.
2. Memudahkan dalam menganalisa/menghitung data, membuat tabel, grafik.

Hal-hal yang perlu diperhatikan dalam pembuatan distribusi frekuensi :
1. Untuk dapat menyusun suatu tabel distribusi frekuensi harus tersedia data. Data yang baru saja dikumpulkan dari lapangan disebut data kasar.

Contoh:
Data masa kerja karyawan UMY adalah sebagai berikut:

2.    Data yang telah disusun ke dalam urutan dari nilai terbesar hingga data terkecil atau sebaliknya disebut array data.

      Contoh:

      Data masa kerja 40 karyawan UMY adalah sebagai berikut:

3. Beda atau selisih antara angka terbesar dengan angka terkecil disebut dengan jarak atau range.

4. Jika array data itu dibagi atas kelompok-kelompok tertentu maka kelompok-kelompok itu disebut dengan kelas.

5. Bilangan-bilangan yang menyatakan banyaknya data yang terdapat dalam setiap kelas disebut frekuensi.

6. Jarak antara kelas yang satu dengan kelas yang lain disebut interval kelas.

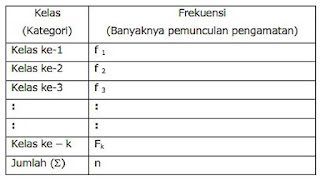
Bentuk Umum Tabel Distribusi Frekuensi

B. Istilah-istilah Dalam Distribusi Frekuensi

1.) Kelas

     Adalah penggolongan data yang dibatasi oleh nilai terendah dan nilai tertinggi dalam suatu kelas.

2.) Interval Kelas 

     Lebar dari sebuah kelas dan dihitung dari perbedaan antara kedua tepi kelasnya. Contoh :

65 – 67 –> Interval kelas pertama

68 – 70 –> Interval kelas kedua

71 – 73 –> Interval kelas ketiga

74 – 76 –> Interval kelas keempat

77 – 79 –> Interval kelas kelima

80 – 82 –> Interval kelas keenam

3.) Batas Kelas (class limit)

      Nilai batas tiap kelas dalam sebuah distribusi frekuensi dan dipergunakan sebagai pedoman guna memasukkan angka-angka hasil observasi ke dalam kelas-kelas yang sesuai.

1. Batas Kelas Bawah (lower class limit) adalah angka pada kolom kelas yang letaknya disebelah kiri.
2. Batas Kelas Atas (upper class limit) adalah angka pada kolom kelas yang letaknya disebelah kanan.

4.) Tepi Kelas (class boundaries/true limits) :

     1. Tepi Kelas Bawah (lower class bounderis)

         Batas kelas pertama yang benar-benar dimiliki oleh distribusi frekuensi tersebut, yaitu batas        kelas bawah dikurangi 1digit dibelakang koma.

     2. Tepi Kelas Bawah (upper class bounderis)

         Batas kelas kedua yang benar-benar dimiliki oleh distribusi frekuensi tersebut, yaitu batas kelas atas ditambah 1digit dibelakang koma.

Tepi atas = batas atas + 0,5

Tepi bawah = batas bawah – 0,5

5.) Lebar kelas

     Lebar kelas = tepi atas – tepi bawah

6.) Mid Point (titik tengah)

      Rata-rata dari kedua batas kelasnya/kelas limitnya. Titik tengah = 1/2 (batas atas + batas bawah)

C. Macam-macam Distribusi Frekuensi

Terdapat dua jenis distribusi frekuensi yaitu:

1.  Distribusi frekuensi numerikal (Numerical frequency distribution)

          Distribusi frekuensi numerikal yaitu distribusi frekuensi yang pembagian kelas-kelasnya berupa angka-angka atau secara kuantitatif. Contoh distribusi frekuensi numerikal yaitu:

Distribusi Frekuensi Numerikal, dibagi menjadi:

a. Distribusi Frekuensi Relatif

    Distribusi frekuensi relatif yaitu distribusi frekuensi yang angka-angka frekuensinya tidak dinyatakan dalam angka-angka absolut tetapi angka-angka relatif atau persentase. Contohnya yaitu:

b. Distribusi Frekuensi Komulatif

     Distribusi frekuensi komulatif terdiri dari dua jenis yaitu :

1) Distribusi frekuensi “kurang dari”

    Distribusi frekuensi “kurang dari” yaitu distribusi frekuensi yang memasukkan frekuensi kelas-kelas sebelumnya. Contohnya yaitu:

2) Distribusi frekuensi “atau lebih”

Distribusi frekuensi “atau lebih” yaitu distribusi frekuensi yang memasukkan frekuensi kelas-kelas sesudahnya. Contohnya yaitu:

2.      Distribusi frekuensi kategoris (Categorical frequency distribution)

      Distribusi frekuensi kategoris yaitu distribusi yang pembagian kelasnya berdasarkan kategori kategori atau secara kualitatif. Contoh Distribusi frekuensi kategoris yaitu:

D. Teknik Pembentukan Distribusi Frekuensi

Ada 2 teknik pembentukan distribusi frekuensi, yaitu:

1. Trial and error

2. Melalui tahap-tahap sebagai berikut:

   a. Menentukan banyaknya kelas

Menentukan banyaknya kelas edapat menggunakan kriterium Sturge

K = 1 + 3,322 log n

K = banyaknya kelas yang sedang dicari

n = banyaknya data

   b. Menentukan besarnya interval kelas (i)

i = r/k

r = Jarak atau range

k = Banyak kelas

Range = angka terbesar – angka terkecil

   c. Menghitung frekuensi data

Contoh Soal

Data berikut ini merupakan nilai ujian Mata kuliah Statistik I dari 25 mahasiswa:

Berdasarkan data tersebut:

1. Buatlah tabel distribusi frekuensi.

2. Tentukan batas kelas, tepi kelas, dan titik tengah.

3. Buatlah distribusi frekuensi relative.

4. Buatlah distribusi frekuensi kumulatif kurang dari.

5. Buatlah distribusi frekuensi kumulatif atau lebih.

Penyelesaian:

1. Tabel distribusi frekuensi

Langkah-langkah pembentukan distribusi frekuensi:

a. Menentukan banyaknya kelas

Menentukan banyaknya kelas dapat menggunakan kriterium Sturges:

K = 1 + 3,322 log n

K = 1+ 3,322 log 25

K = 1+ 3,322 (1,398)

K = 5,644

K = 6 (dibulatkan)

b. Menentukan besarnya interval kelas (i)

i = r/k

r = Jarak atau range

k = Banyak kelas

Range = angka terbesar – angka terkecil

Angka terkecil = 27

Angka terbesar = 94

Range = 94 – 27 = 67

Banyaknya kelas = 6

i = 67/6 = 11,17 = 12 (dibulatkan)

c. Membuat tabel distribusi frekuensi

Penyajian distribusi frekuensi

2. Tentukan batas kelas, tepi kelas, dan titik tengah

3. Distribusi frekuensi relatif

Frekuensi kelas 1 = 1/25 x 100 = 0,08 = 4 %

Frekuensi kelas 2 = 3/25 x 100 = 0,08 = 12 %

Frekuensi kelas 3 = 5/25 x 100 = 0,20 = 20 %

Frekuensi kelas 4 = 8/25 x 100 = 0,32 = 32 %

Frekuensi kelas 5 = 5/25 x 100 = 0,20 = 20 %

Frekuensi kelas 6 = 3/25 x 100 = 0,12 = 12 %

4. Distribusi frekuensi kumulatif kurang dari

5. Distribusi frekuensi kumulatif atau lebih

E. Grafik Distribusi Frekuensi

1. Histogram

Histogram adalah diagram batang yang lebarnya menunjukkan interval kelas, sedangkan batas-batas tepi batang merupakan tepi bawah dan tepi atas kelas, dan tingginya menunjukkan frekuensi pada kelas tersebut. Jika pada diagram batang, gambar batang-batangnya terpisah maka pada histogram gambar batang-batangnya berimpit. Histogram terdiri dari 2 sumbu, sumbu vertikal sebagai skala frekuensi sedangkan sumbu horisontal untuk skala kelas.

Contoh :

Diketahui nilai ujian 40 siswa di SMA Jaya Selalu. Tentukan histogram daftar distribusi frekuensi dan frekuensi relatifnya.

Maka histogramnya

2. Poligon Frekuensi

Poligon Frekuensi yaitu penggambaran distribusi frekuensi dalam bentuk garis yang menghubungkan titik-titik tengah kelasnya sebagai skala kelas. Jenis lain dari poligon frekuensi adalah kurva frekuensi, yaitu penggambaran distribusi frekuensi dalam bentuk garis, dimana luas daerah di bawah kurva kurang lebih sama dengan luas histogram frekuensinya. Kurva frekuensi dapat digambarkan dengan memanfaatkan histogram frekuensi dengan menggunakan angka-angka tepi kelas sebagai skala kelas, dengan menghubungkan titik-titik tengah masing-masing balok.

Contoh :

Berikut ini upah karyawan (dalam ribuan rupiah) per minggu dari sebuah perusahaan.

Hasil akhir dari histogram dan poligon frekuensi dari tabel distribusi frekuensi di atas dapat dilihat pada gambar berikut.

3. Ogive Curve atau Kurva Ogive

Kurva ogive merupakan diagram garis yang menunjukkan kombinasi antara interval kelas dengan frekuensi kumulatif. Kurva ogif menunjukkan frekuensi kumulatif pada setiap tingkat atau kategori. Sumbu horizontal pada kurva ogif menunjukkan tepi interval kelas dan sumbu vertical menunjukkan frekuensi kumulatif. Kurva ogif memudahkan kita untuk melihat frekuensi kumulatif baik dalam bentuk nilai absolute maupun nilai relative pada tingkat atau interval tertentu.

Daftar distribusi kumulatif ada dua macam, yaitu sebagai berikut :

a. Daftar distribusi kumulatif kurang dari (menggunakan tepi atas)

b. Daftar distribusi kumulatif lebih dari (menggunakan tepi bawah)

Contoh :

Data upah karyawan sebelumnya dapat digambarkan ogivenya. Akan tetapi sebelum itu, buat terlebih dahulu tabel distribusi frekuensi kumulatifnya.

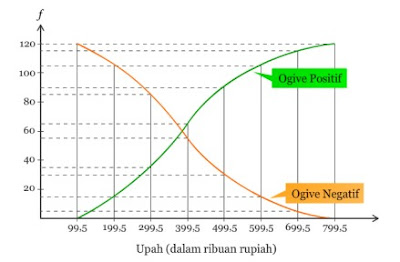
Dari tabel distribusi frekuensi kumulatif di atas, dapat digambarkan ogive seperti pada diagram berikut.

F. Model-model Populasi

Poligon frekuensi yang merupakan garis patah-patah dapat didekati oleh sebuah lengkungan halus yang bentuknya secocok mungkin dengan bentuk poligon tersebut. Lengkungan yang didapat dinamakan kurva frekuensi. Jika semua data dalam populasi dapat dikumpulkan lalu dibuat daftar distribusi frekuensinya dan akhirnya digambarkan kurva frekuensinya, maka kurva ini dapat menjelaskan sifat-sifat karakteristik populasi. Kurva ini merupakan model populasi yang akan ikut menjelaskan ciri-ciri populasi. Dalam praktek, model populasi ini biasanya didekati oleh atau diturunkan dari kurva frekuensi yang diperoleh dari sampel reprenentatif yang diambil dari populasi.

Untuk keperluan teori dan metode yang lebih lanjut, metode populasi ini dituangkan dalam bentuk persamaan matematik. Beberapa diantaranya akan dibahas kemudian. Pada saat sekarang hanya akan diberikan bentuk kurva untuk model populasi yang sering dikenal. Diantaranya model normal, simetrik, positif atau miring ke kiri, negatif atau miring ke kanan, bentuk J dan U.

1. Model normal, yang sebenarnya akan lebih tepat digambarkan berdasarkan persamaan matematiknya. Bentuk model normal selalu simetrik dan mempunyai sebuah puncak. Kurva dengan sebuah puncak disebut unimodal.

2. Model simetrik, di sini juga unimodal. Perhatikan bahwa model normal selalu simetrik tetapi tidak sebaliknya.

3. Model positif menggambarkan bahwa terdapat sedikit gejala yang bernilai makin besar.

4. Model negatif terjadi sebaliknya. Soal ujian yang terlalu mudah sehingga banyak peserta yang mendapat nilai baik menggambarkan model negatif.

5. model berbentuk J ini terdapat dalam dunia ekonomi, industri dan fisika.

6. Model bentuk U menggambarkan mula-mula terdapat gejala bernilai kecil, kemudian menurun sementara gejala bernilai besar dan akhirnya menaik lagi untuk nilai gejala yang makin besar.

Model dengan lebih dari sebuah puncak disebut multimodal. Kalau hanya ada dua puncak disebut bimodal.

DAFTAR PUSTAKA

Parmita, Vebriana. 2013. Distribusi Frekuensi dan Grafik. (Online).            (http://vebrianaparmita.wordpress.com/2013/09/21/bab-iii-distribusi-frekuensi-dan-grafik/, dikunjungi 01 Oktober 2014).

Suharyadi, & Purwanto. (2009). In Statistika untuk Ekonomi dan Keuangan            Modern. Jakarta: Salemba Empat.

Sudjana. (1991). In Statistika. Bandung: Tarsito.

Smartstat. 2010. Distribusi Frekuensi. (Online).        (http://smartstat.wordpress.com/2010/03/29/distribusi-frekuensi/,dikunjungi 01 Oktober 2014).